Sidebar
Table of Contents
Optical properties of ice clouds
Development of new parameterization
/home/claudia/yang_hong_emde
Script to calculate optical properties from single scattering data: calc_opt_prop.py
Synchronize with lx321:
rsync -rdltvu yang_hong_emde emde_cl@lx001.pa.op.dlr.de:/net/lx321/export/home/emde_cl/
Single scattering data
Single scattering data calculated by Gang Hong using the codes by Ping Yang:
/home/claudia/yang_hong_phamat/88_bands
Format of data:
Wl(um) Size(um) Volume(um3) Area(um2) Extioneff Albedo GG F-delta Theta(0-180)
(separate files for each phase matrix element)
Size distribution data
Data needs to be integrated over size distribution.
Gamma distributions suggested by Evans
This method has been applied to derive HEY parameterisation for libRadtran.
From SHDOM documentation:
<latex> n®=N_0 r^\alpha \exp(-\frac{\alpha+3}{r_{\rm eff}}) </latex>
Here r is the mass equivalent radius or effective size (Yang et al., 2005)
<latex> r=\frac{3V}{2A} </latex>
where V is the volume of the particle and A is the cross section.
Evans et al. 1998 study the radiative properties (submm range) of ice clouds depending on measured size distributions of the FIREII experiment. In the measurements alpha varies from -0.5 to 7 (larger values for smaller temperatures/ smaller particles). Setting alpha=1 was ok. to model radiative properties correctly.
We now keep alpha=1 and iteratively find the parameters lambda, that result in the desired effective radii (5,10,15,…,90). The resulting optical properties (found by integration over the gamma distributions) are similar to the ones found by integration over the 30 measured size distributions (see below). The main differences are found in the asymmetry parameter, which is systematically larger for the gamma distributions than for the measured distributions, indicating that the gamma distributions underestimate the amount of small particles (small asymmetry parameter). But in all cases the optical properties obtained from the gamma distributions are in the range of the measured distributions.
Gamma distributions fitted by Heymsfield et al., 2002
The Gamma-distributions by Heymsfield et al. (2002) that have been fitted to in-situ measurements of the TRMM field campaigns are defined similarly to Evans et al. (1998).
<m 12> N = N_0 D^\mu \exp(-\lambda D) </m>
T {\rm smaller} 27^\circ:
\lambda=24.0 \exp(-0.049 T)
T \ge 27^\circ: \lambda=6.8 \exp(-0.096 T)\\[1ex]
\mu=0.13\lambda^{0.64}-2\\[1ex]
r_e=\frac{159 \Gamma(3.2+\mu)}{\Gamma(2.8+\mu)\lambda^{0.41}}
Here D is the maximum (!) dimension of the particles. More or less consistently with Evans et al. 1998, the parameter mu varies from about -1 to 5.
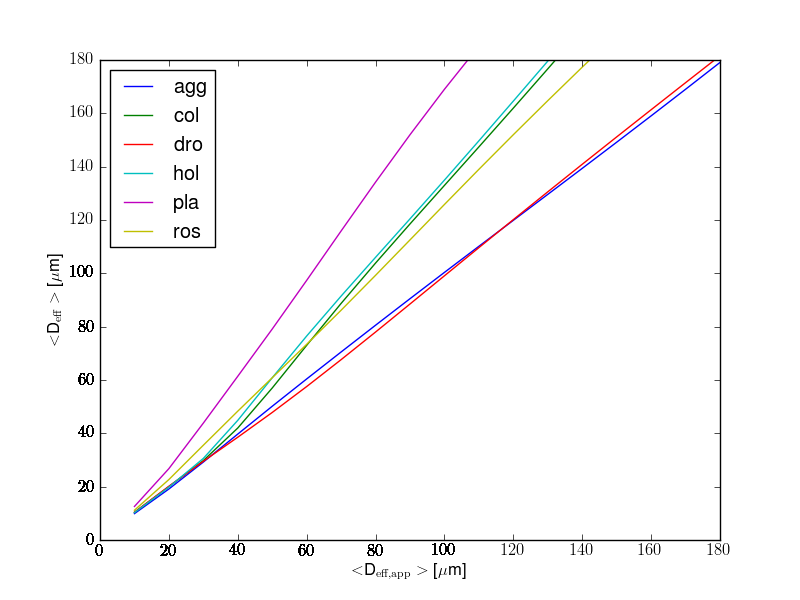
Applying these size distributions to the various shapes gives effective radii in the range from approx. 20 to 100 microns, for droxtals only effective radii larger than about 70 micron which shows that probably no droxtals have been measured. As stated, small particles were not fitted. Comparing the obtained effective radii to a fit of for effective radius given in Heymsfield 2002 (based on measured IWC and A) gives a plausible result if one assumes a particle mixture (droxtals excluded).
30 size distributions, Key 2002
The 30 size distributions cover the following ranges of Reff:
| shape | min reff | max reff |
|---|---|---|
| droxtal | 9.5 | 293.7 |
| aggregate | 3.4 | 105.8 |
| solid column | 5.9 | 91.4 |
| hollow column | 4.9 | 76.2 |
| plate | 4.8 | 50.1 |
| bullet rosette | 3.0 | 47.6 |
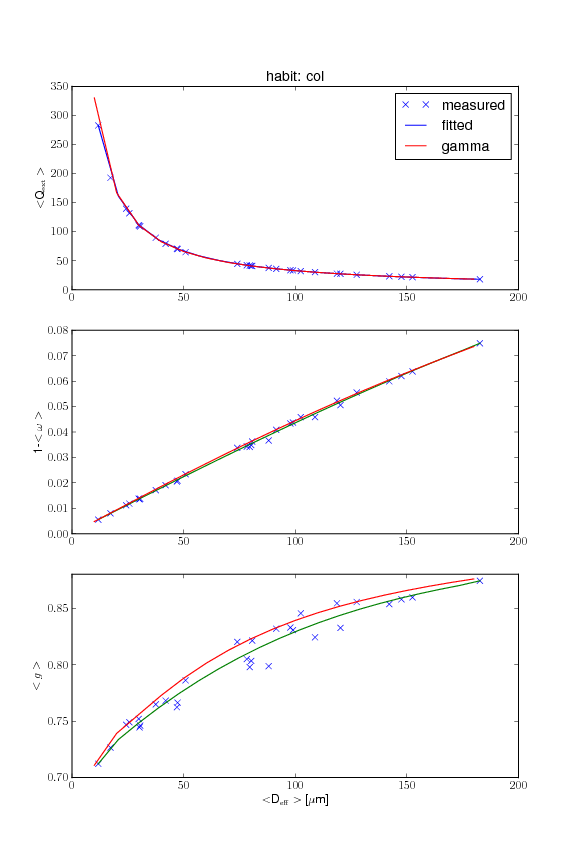
It is possible to get a fit for the optical properties extinction, single scattering albedo, and the asymmetrie parameter as a function of effective radius:
But for the phase functions it is problematic. In the forward scattering region, the value of the phase function extends over several orders of magnitude. The fit returns negative values for the small Reff values. These negative values can be avoided by fixing the phase function of the smallest Reff to the value obtained by the size distribution corresponding to the smallest Reff. But this results in ugly discontinuities for some scattering angles and a strange behaviour in the forward scattering region. The maximum is not at 0 degrees scattering angle but slightly larger. Therefore it is not a good idea to fit each angle in the phase function separately.

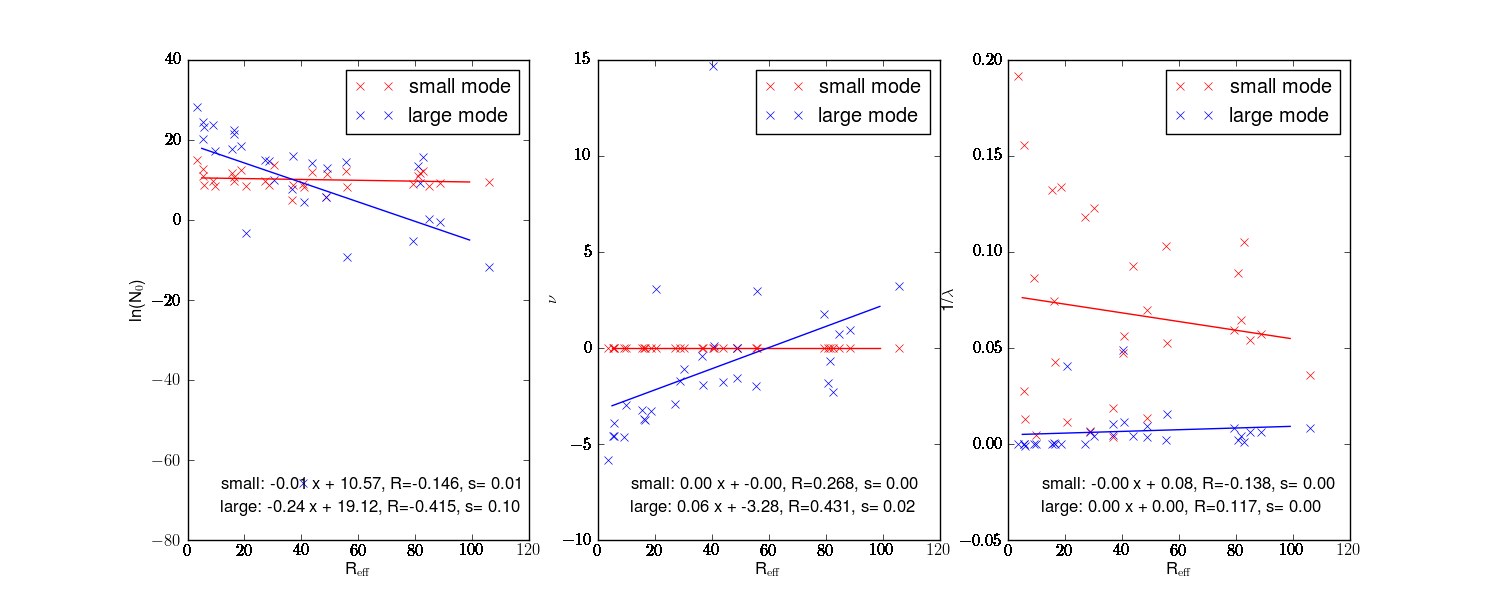
Another possiblity is to use the measured size distribution and fit them to gamma distributions. It turned out that most of the distributions can only be fitted by bimodal gamma distribution. The fit of the gamma distribution parameters against reff is also not very nice (large scattering). Results in /yang_hong_emde/30_dist.
Ivanova (2001) has generated a parameterization for ice cloud bimodal size-distribution. Here the parameters depend not only on Reff, but also on IWC, T, particle falling speed … My conclusion from the study with the 30 size distributions is that it is probably not possible to generate a realistic parameterization for the size distribution that depends only on the effective radius.