Matthias Sommer

• Atmospheric Data Assimilation
• Ensemble Kalman Filter

• Observation impact in convective scale data assimilation
• Model error in data assimilation: Adaptive inflation methods

Model and sampling error for use in ensemble data assimilation systems In order to compute optimal weights of background and observations, any data assimilation scheme needs accurate estimates of the corresponding error covariance matrices. In ensemble Kalman filters, the background error covariance matrix is sampled by an ensemble of geophysical model runs. However, since any numerical model itself suffers from errors and also since the number of ensemble members typically used is much smaller (10-100) than the dimension of the phase space of a typical atmopheric ciruclation model (>10^6), the entire uncertainty can not be captured this way.

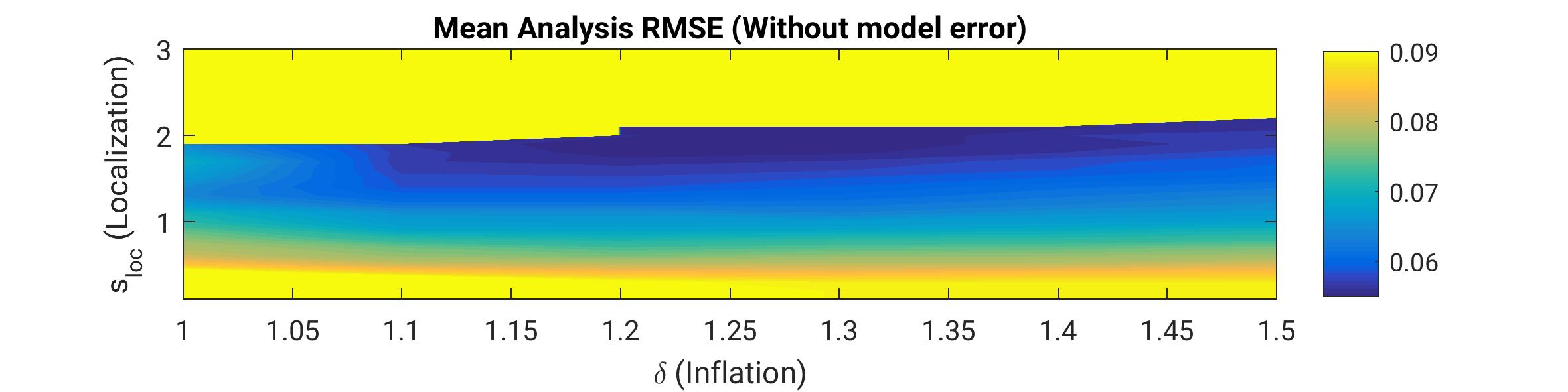
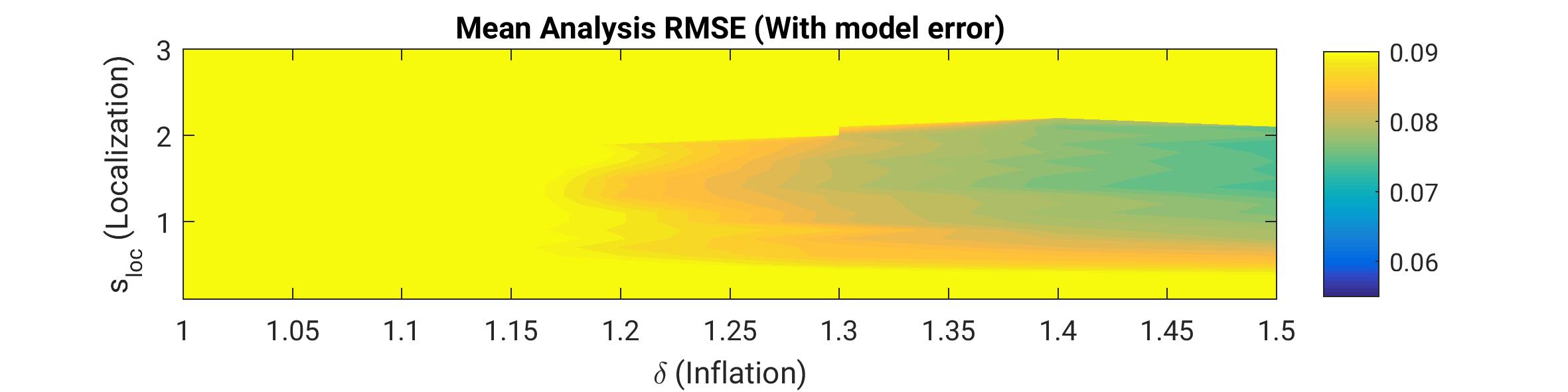
This work unit investigates methods for correcting these deficiencies as for example localization, as well as multiplicative and additive inflation. While the former two are designed to address the sampling error, the latter deals with model error itself as illustrated in Figure below. In an perfect model experiment with a low-dimensional toy model (Lorenz'96) an optimal combination of localization and multiplicative inflation yields the lowest error (blue region in the upper panel). If however model error exists, the multiplicative inflation factor becomes very large while the RMSE remains higher (lower panel) than in perfect model experiment. As an alternative approach, additive inflation can be implemented to overcome that shortcoming. This approach is ongoing research togehter with an implementation for the regional weather forecasting model COSMO of German Weather Service (Deutscher Wetterdienst DWD).

• M. Sommer & P. Névir (2009). `A conservative scheme for the shallow-water system on a staggered geodesic grid based on a Nambu representation'. Quart. J. Roy. Meteor. Soc. 135:485-494. (Link)
• P. Névir & M. Sommer (2009). `Energy-Vorticity Theory of Ideal Fluid Mechanics'. J. Atmos. Sci. 66:2073-2084. (Link)
• S. Shin, M. Sommer, S. Reich, P. Névir (2010). `Evaluation of three spatial discretization schemes with the Galewsky et al. test'. Atmospheric Science Letters 11:223-228. (Link)
• M. Sommer & S. Reich (2010). `Phase space volume conservation under space and time discretization schemes for the shallow-water equations'. Mon. Wea. Rev. 138:4229-4236. (Link)
• M. Sommer (2010). `Numerische und geometrische Aspekte der Energie-Wirbel-Theorie'. Doctoral thesis, Freie Universität Berlin. (Link)
• M. Sommer, K. Brazda & M. Hantel (2011). `Algebraic construction of a Nambu bracket for the two-dimensional barotropic vorticity equation'. Phys. Lett. A 375:3310-3313, arXiv: 1102.1298. (Link)
• M. Sommer, K. Brazda & M. Hantel (2012). `Statistical mechanics for conservative discretizations of two-dimensional incompressible flow'. Met. Z. 21:371-384. (Link)

2019

• Zeng Y., T. Janjic, M. Sommer, A. de Lozar, U. Blahak, A. Seifert, 2019, Representation of model error in convective-scale data assimilation: additive noise based on model truncation error, J. Advances in Modelling Earth Systems, 11, 752-770, (link).