Today finished the work on a new external solver for PPRTS, namely a wrapper for the MonteCarlo Raytracer RayLi from Tobi. This allows to compute irradiances and absorption in the cartesian mesh solvers (PPRTS) aswell as take virtual photographs of the simulations.
The main reason to implement the raytracer was to be able to do MonteCarlo benchmark simulations on the native grid that the TenStream uses. For rectangular cartesian meshes we used to do the benchmark simulations with MYSTIC but this approach is cumbersome in case of terrain-following meshes as we encounter them e.g. in WRF.
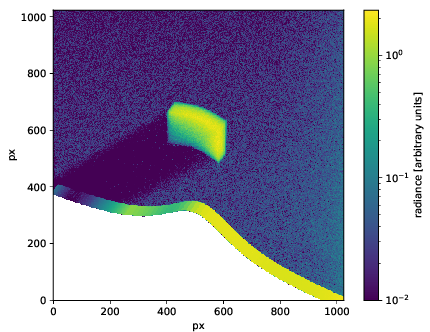
The following image depicts a 2D test example from <tenstream>/examples/pprts_hill/ with a pressure deficit in the middle of the domain (resulting in a gaussian hill elevation).
Giving the options (determined from a visit camera view)
-rayli_snapshot
-rayli_snap_photons 1e7 \
-rayli_snap_Nx 1024 \
-rayli_snap_Ny 1024 \
-visit_image_zoom 5.5 \
-visit_parallel_scale 15e3 \
-visit_focus 150,3200,2000
-visit_view_normal 0.7070747611534114,0.2327674681159244,0.6677309247943728 \
-visit_view_up -0.6351822897895342,-0.2059442342233124,0.744399376093168 \
Computing irradiances and absorption with MonteCarlo
can be done with
-pprts_use_rayli
-rayli_cylic_bc
-rayli_diff_flx_origin 0,0,-inf
Which sets the solver to use MonteCarlo with cyclic boundary conditions.
The diff_flx_option sets the distinction for upward and downward irradiance, i.e. a dot_product between the ray and this vector determines if the ray is counted as upward or downward irradiance.
This is necessary to get reliable results as the default is set to the origin in case of spherical coordinates.
For a full set of options and how to process the output, have a look at <tenstream>/examples/pprts_hill/hill.sh.
Technical details on parallelization
Implementing a fully scalable Raytracing solver with domain decomposition is hard. In fact, I don’t have an idea how to I’d would start to tackle the issues of load balancing which arise in heterogeneous cloudy scenes. Anyway, the approach that the current RayLi integration takes is a semi scalable solution that should be able to work up to medium sized problems.
Let’s assume Tenstream runs on a MPI-communicator called ts_comm and is split with TYPE_SHARED into subcommunicators which have a shared memory section. We then create a sequential plexrt grid (triangular surface solver) on each rank with sub_comm_id==0 with twice as many wedges as we have boxes in the cartesian mesh. Subsequent vec_scatters of optical properties and albedo from all ranks to the sub_comm_roots enable shared-memory parallel (threaded) MonteCarlo simulations.
An example: If we have 16 ranks per node and 3 nodes, the ts_comm consists of 48 ranks. And the sub_comm naturally has 16 ranks on each node. I.e. we may have the following rank numbering
| ts_comm_id | sub_comm_id | runs RayLi |
|---|---|---|
| 0 | 0 | * |
| 1 | 1 | |
| 15 | 15 | |
| 16 | 0 | * |
| 17 | 1 | |
| … |
Indeed, this approach at least triples the global memory footprint per node but is the best we have at the moment.