Influence of the initial guess on the number iterations

Testing the influence of the initial guess on the number of iterations needed

The setup is as follows:

Start a ex_plex_rrtmg_fish simulation with a fish (torus) mesh with 553 columns and 65 levels and solve for direct radiation. The spectral integration goes over the 112 solar and 140 thermal spectral bands of RRTMG and the initial solar zenith angle is $0^\circ$.

Then we iterate over time and for the solar examination only the solar zenith angle is changed by $1^\circ$ per iteration. In case of thermal examinations, we perform a circular shift of the cloud field by 1 comlumn for each iteration. The iterative solver is a outer Krylov solver FGMRES with an incomplete LU decomposition on each mpi process of which we run on a single workstation machine. For each iteration we sum up the total number of iterations the solver needed over all bands, i.e. for each timestep. We then conduct the experiment three times

zero — i.e. where we do not use the last times solution and rather start with $\vec x = 0$
initial_guess — where we use the last timestep ($0.25^\circ$ earlier) as the initial guess
hegedus_trick — where the last timestep solution is rescaled according to hegedus formula

Hegedues Formula from Liesen Strakos, 2019, Krylov Subspace Methods eq. (5.8.16)

$$\zeta_{min} = \frac{ b * Ax_p }{ \left\Vert Ax_p \right\Vert^2 }$$

where $x_p$ is the solution of the last timestep and the initial guess $x_0$ is rescaled according to:

$$x_0 = \zeta_{min}x_p$$

After the implementation from krypy->utils.py

Ax0 = A * x
z = M * Ax0
znorm2 = inner_product(z, Ax0)
if znorm2 >= 1e-15:
  gamma = inner_product(z, b) / znorm2
  x *= gamma

or in Fortran with PETSc respectively:

call MatMult(A, x, Ax0, ierr)
call MatMult(P, Ax0, z, ierr)

call VecDot(z, Ax0, znorm, ierr)
call VecDot(z, b, norm, ierr)

if(znorm.gt.epsilon(znorm)) call VecScale(x, norm / znorm, ierr)

where A ist the system matrix, b the source vec of radiation, x the initial guess

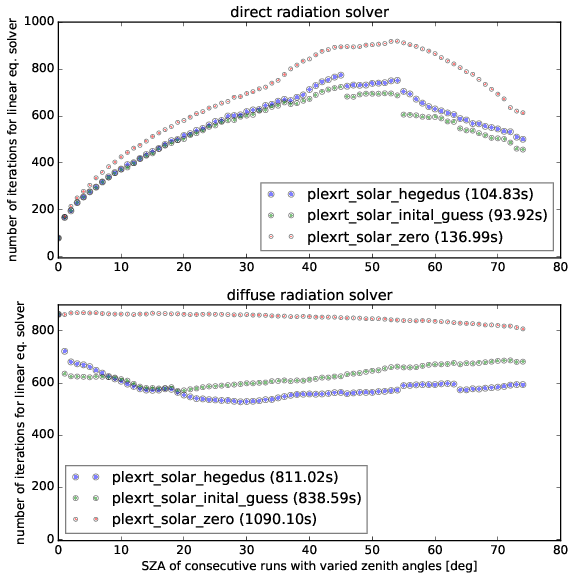
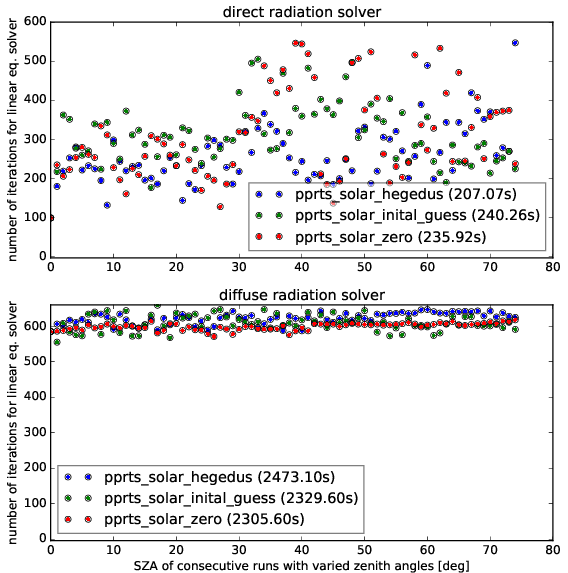
Results: Iteration counts for various experiments

4 Minute intervals:

In brackets behind the legend, we find the total time that the simulation of all iterations have taken, i.e. something like the dirunal cycle. We see that in our case supplying the last solution as first guess has generally a beneficial effect on the number of iterations aswell as on the time-to-solution. E.g. for the diffuse solver, we only need about half as many iterations and particularly the hegedus renormalization seems to be beneficial. Through the use of the initial guess, we can speed up the simulations by up to 40%. Furthermore, the use of the hedegus normalization yields better results in the case of diffuse radiation whereas in the case of direct radiation it might even make convergence worse and is hence not recommended to use there.

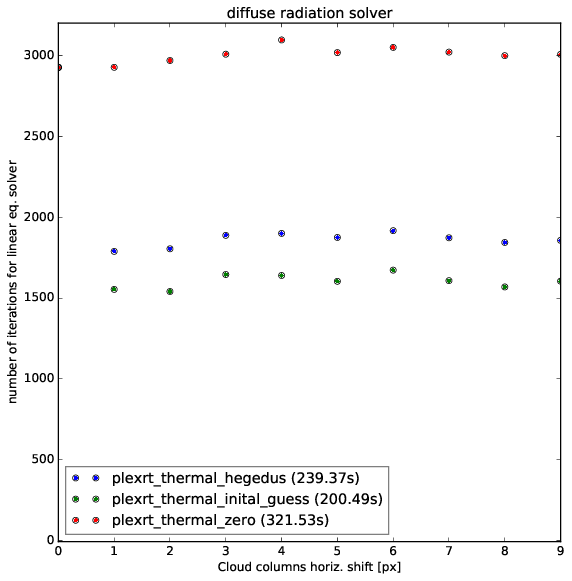
Following for thermal computations where the cloud field is shifted each time by 1 column.

No gain for hedegus visible but the initial guess gives a better solution time by about 35%.

Appendix:

Graph for solar pprts computations

4 Minute intervals: